Carmenta Engine includes an extension for terrain vehicle routing that models terrain as a graph, consisting of nodes connected by edges. This terrain information is derived from raster data, where each pixel is represented as a node, resulting in a graph with a notably regular structure.
A key task within this framework is solving the single-source shortest path (SSSP) problem. This involves determining the least-cost paths from a given source node to all other nodes in the graph. SSSP problems are prevalent in various applications, such as generating isochrone maps, planning supply missions, and addressing “traveling salesman” problems.
While the most common algorithm for SSSP is reasonably efficient, it is not well-suited for parallelization. Although parallel algorithms have been explored, they are typically designed for general graphs. Fjellborg’s master’s thesis focused on implementing and testing SSSP algorithms using GPU-parallelism, leveraging the regular structure of the terrain graph.
Figure: Two images showing the velocity raster of the Lake Tahoe dataset, with the computed distance vector below and the original velocity raster above. Lighter colors denote a higher velocity and lower distance to start respectively. Black and white denote untraversable and unknown (no data) or unreached cells.
Routing is a problem with diverse applications, multiple problems from several fields can be formulated as general graph problems, one of the most intuitive being vehicle routing, graphs denoting positions (nodes) and their connecting paths, and solved using some type of pathfinding. Implementing pathfinding for general graphs on the parallel architecture of the GPU poses several challenges, including limited memory, work balancing, synchronization, as well as branching.
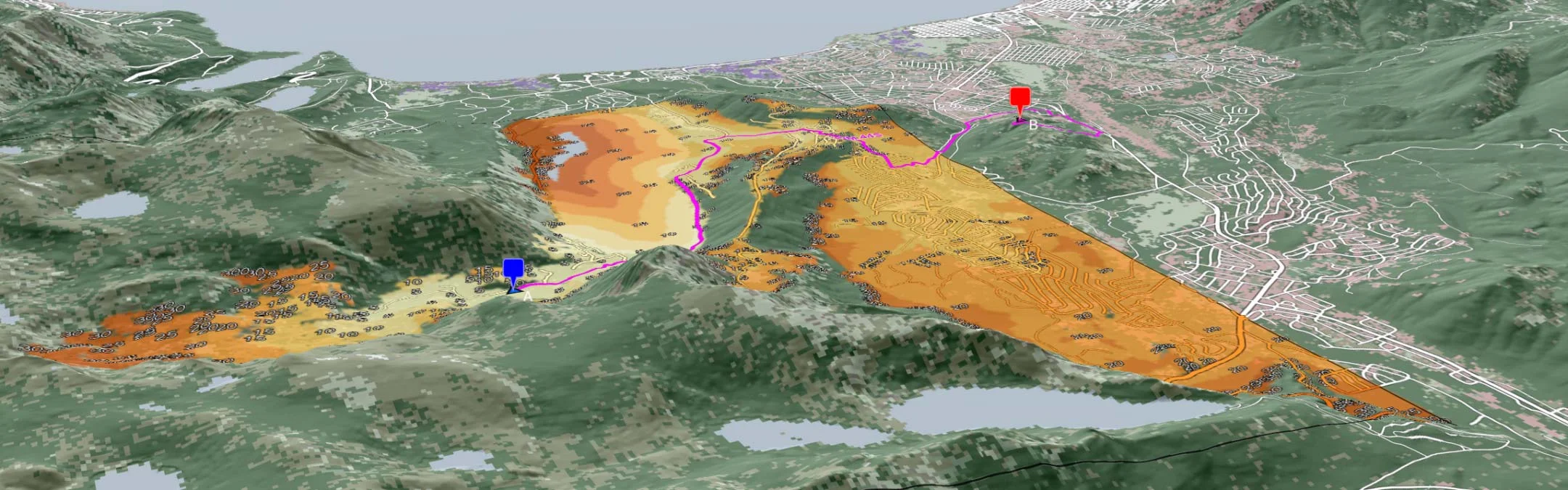
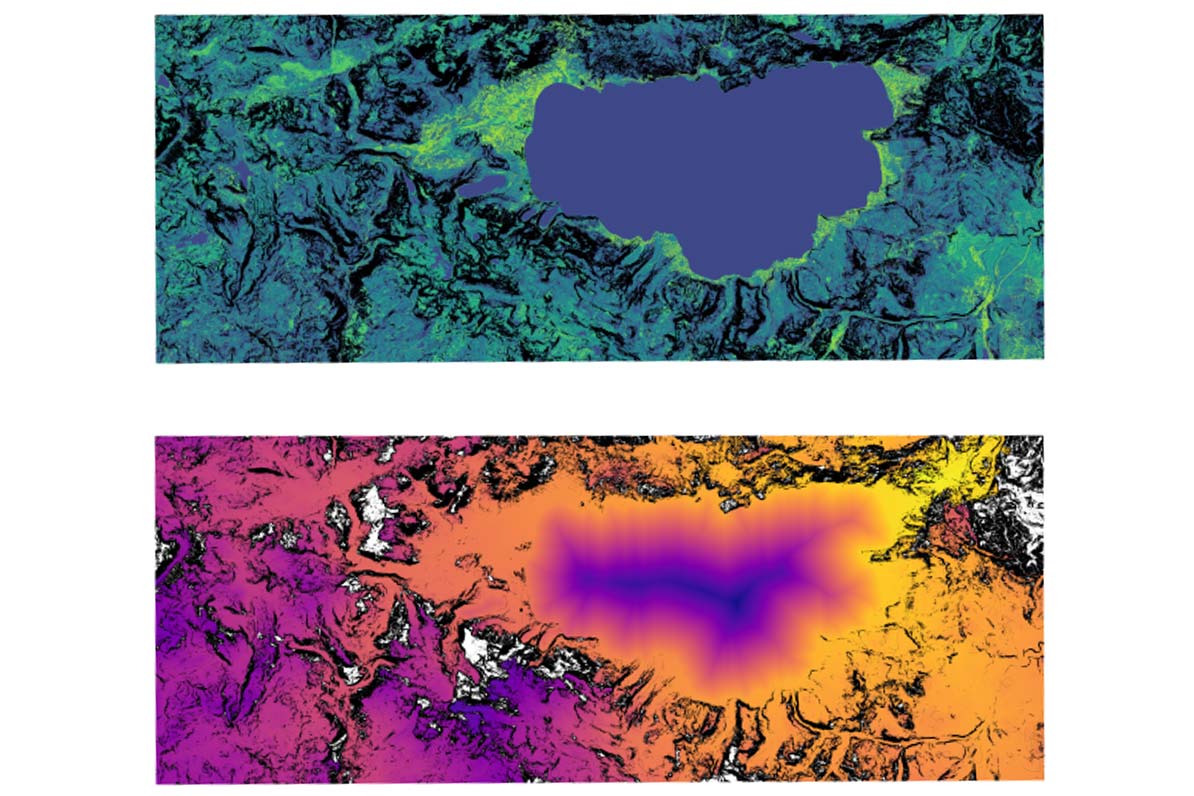
This degree project compares and evaluates several algorithms and methods for computing path isochrones, the complete set of shortest paths to everywhere from a given starting position for large terrain rasters on the GPU. Terrain rasters in this context entails uniform grid data where each grid cell encodes either a traversal cost or the inverse thereof, traversal speed for a specific vehicle. The goal is to find or improve the methods existing for general graphs, optimizing for this specific type of graph. Two implementations are presented, both variations of the commonly used delta-stepping method, one for graphs too large to fit in memory with local pathfinding until convergence, and one for smaller graphs, equivalent to the former, but with the whole graph rather than a subset.
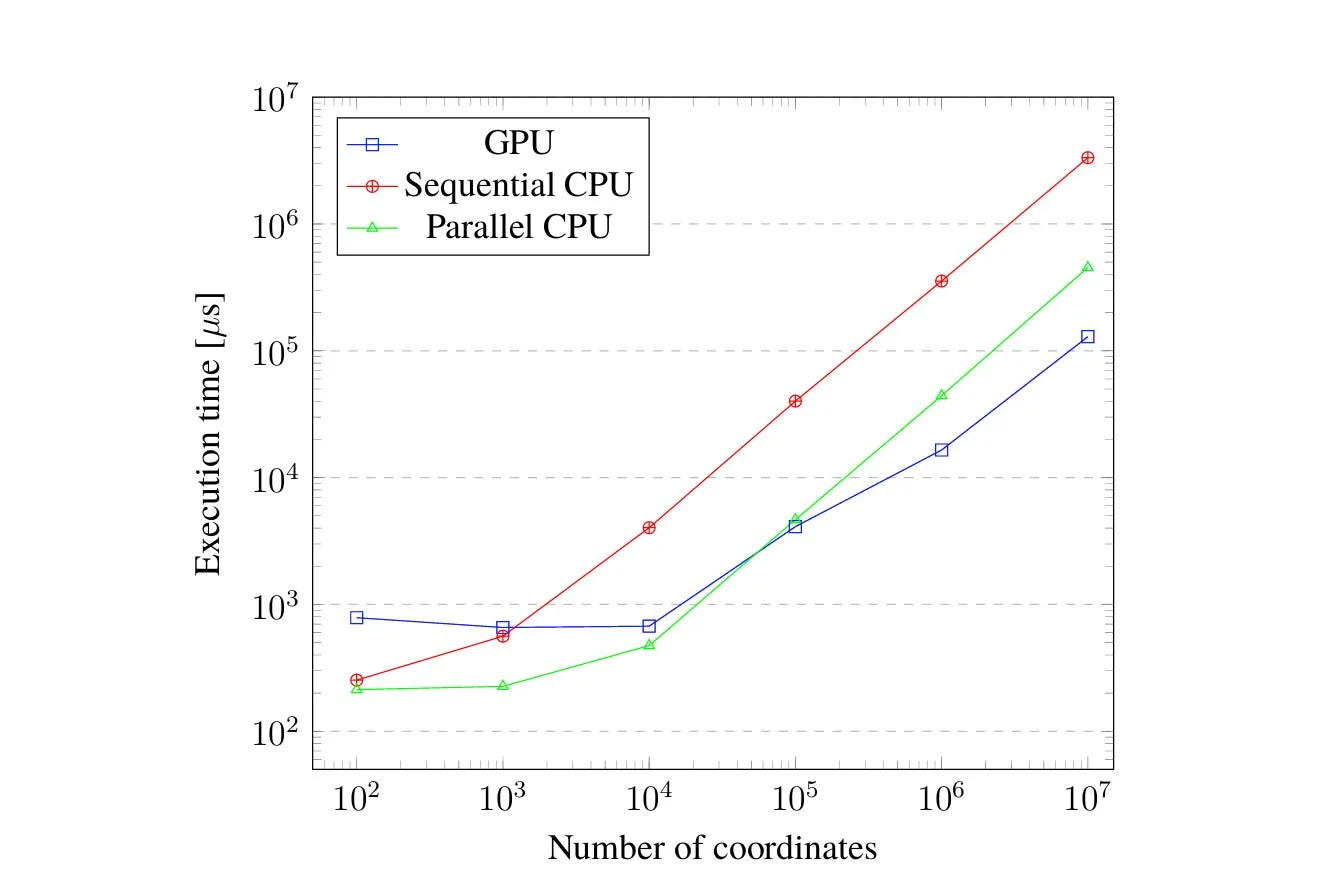
The results show that specializing implementations to function on the native format of the grid is more effective than converting to the more commonly used CSR format, due to required data movement, and constant degree of the cells. Synchronization and data movement play a significant role in the possible speedup of pathfinding on these type of graphs. The structure of the graph itself plays the most significant role, larger and more connected graphs allows for a larger speedup. The developed implementations achieve a speedup of around 10 for large connected graphs, around 5 for the average case, and on par with a sequential reference implementation in the worst case.
Fjellborg, Joakim. An implementation and performance evaluation of parallel algorithms for off-road vehicle routing on the GPU (2024).
By leveraging parallel processing, this master's thesis examines performance gains and usability improvements, making advanced geospatial analysis more accessible without requiring deep GPU programming expertise.
Read more
Collaborative single-display teamwork without any widget or button. A case study using Carmenta Engine. This thesis introduced a new form of interfacing with the Carmenta Engine on touch screen. Its results show that through using the technique of hand chords, several users can work with the one large touchscreen simultaneously.
Read more