Technical Whitepaper

Optimizing Firing Position Usage for Survivability and Effectiveness in Artillery Shoot-and-Scoot Tactics

In shoot-and-scoot tactics, a common rule is that artillery units should not reuse firing positions; a more cautious rule is that they should not even pass near an old firing position when relocating.

The paper introduces this cautious rule to define a new variant of the traveling salesman problem: maximizing the number of firing positions while minimizing travel time under strict movement constraints. To tackle this, we develop greedy and randomized heuristic algorithms, along with methods to reduce problem size using graph theory. Our results show that repeated randomized runs yield good solutions quickly, and that problem reduction can further boost performance.

This highly technical paper was originally presented at the 2025 Ground Vehicle Systems Engineering and Technology Symposium (GVSETS) in the US. It was awarded Best Paper at the Autonomy, Artificial Intelligence & Robotics track at GVSETS 2025.

Authors: Thomas Jonsson Damgaard and Dr. Mikael Rittri from Carmenta Geospatial Technologies.

Introduction

Artillery has always played an important role in warfare, including modern warfare. “UAVs haven’t made artillery irrelevant, but in many cases they have made artillery systems more effective and precise”, a quote from Harry Lye. Lye highlights the importance of artillery systems in suppressing hostile forces, such as SEAD missions (Suppression of Enemy Air Defenses). However, Lye stresses that they are also vulnerable on the battlefield. We intend to build algorithms that improve the survivability of artillery systems in active combat by choosing which firing positions to use and in what order.

Shoot-and-Scoot Tactics

The advantages of artillery systems are their long range and their ability to fire beyond visual line of sight, allowing them to surprise the enemy. However, after the first rounds have been fired, the enemy can use counter-battery radar systems to analyze projectile trajectories to determine their source and respond with their own artillery, and the response may take only 5 to 12 minutes.

For this reason, artillerymen use shoot-and-scoot tactics: First they find a good position to fire from. Then after firing a number of rounds, they quickly relocate about 500 meters to a different area to hide from incoming returned fire. Finally, they will move to a new position and repeat the process. By applying shoot-and-scoot tactics, Ukrainians can operate their howitzer fleet in a safer way.

There are modern artillery systems, such as the Archer system, that are designed for speed by using automatic reload systems and rapid emplacement and displacement of guns, and by being mounted on flexible terrain vehicles. These are the key elements of effective shoot-and-scoot efforts.

Conclusion

The traveling artilleryman problem is NP-hard, but we have developed two heuristic algorithms, Nearest Neighbor and Random Neighbor, that can produce good solutions reasonably fast for problems of modest size. We have also developed a simple “overgreedy” algorithm that calculates a lower bound of the solution cost for a given cardinality (number of positions used).

We have also discovered a way to analyze conflicts between positions in a TAP instance via maximum independent sets. In this way, one can find positions that cannot possibly be used by an optimal solution, and by removing these, one can improve the performance of the heuristic algorithms.

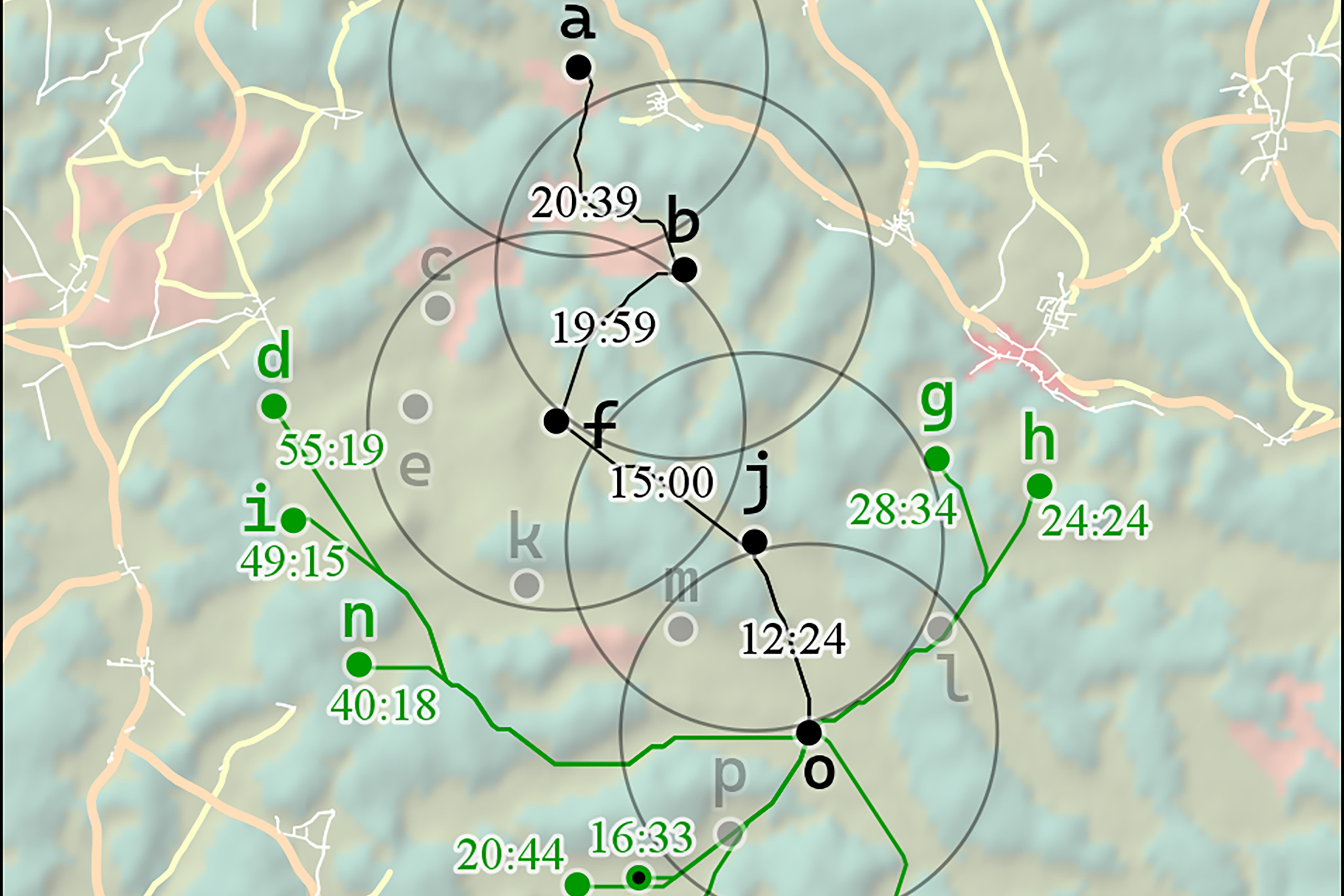
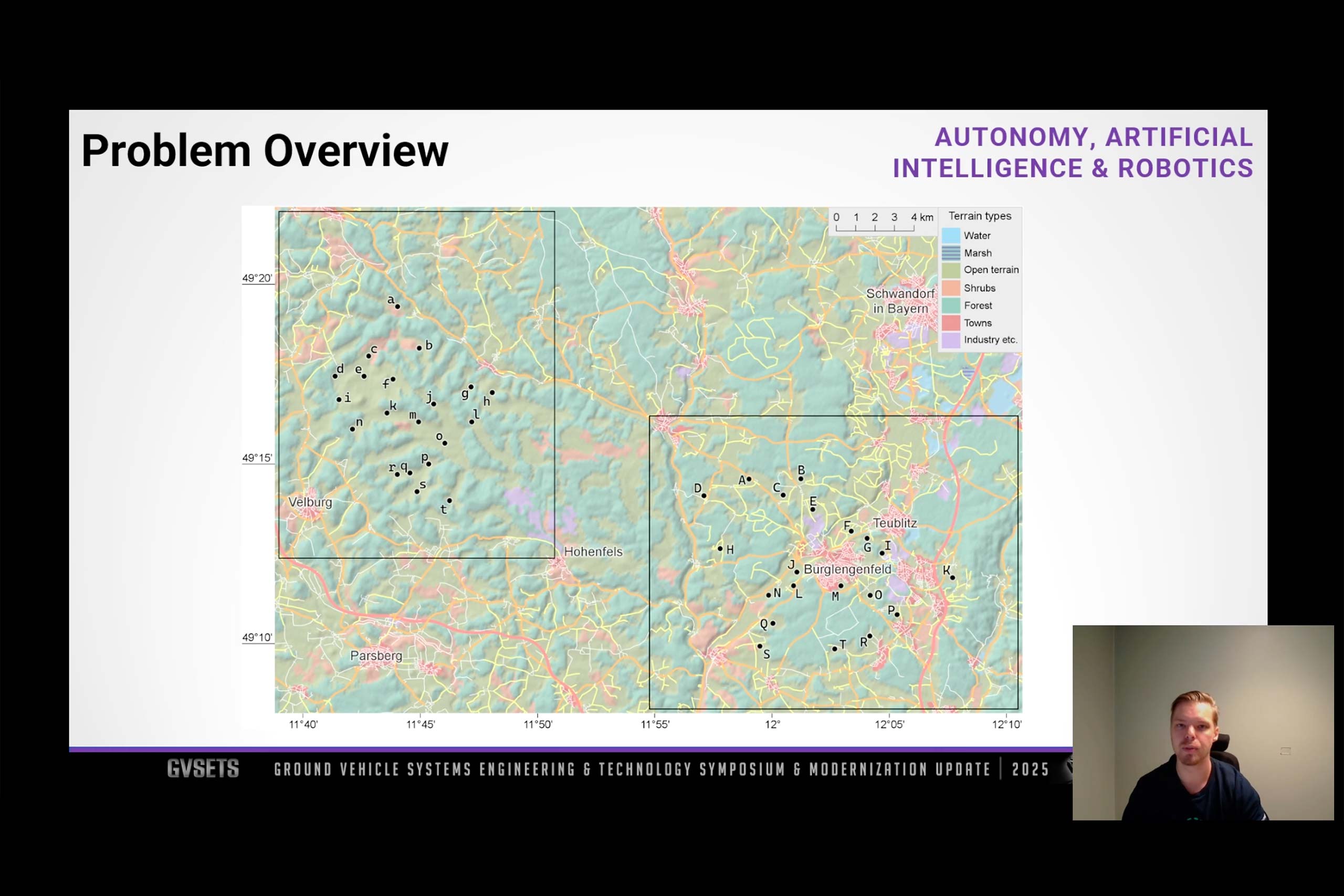
We have tested our algorithms and our conflict analysis on three TAP instances with 20 positions each, and measured running time and solution quality. Running our Nearest Neighbor algorithm or Random Neighbor algorithm once on one of our TAP instances takes about 3 seconds in our implementation, but in general the time will depend on many factors like the number of positions, the size of the search area, and the terrain resolution.

Measuring solution quality was problematic. For a solution of optimal cardinality (the number of positions used), we would have preferred to define its quality as the percentage by which its cost exceeds the cost of an optimal solution. But we could not measure that percentage, since we do not know the optimal solutions.

We do have the simple algorithm that can calculate a lower bound for the cost of an optimal solution, so we can measure the percentage by which the cost of a solution exceeds the lower bound, but we believe that our lower bounds are not very tight. So, instead of comparing with the optimal solution or a lower bound, we compare with a “winning” solution: the best solution we have found by running the Random Neighbor algorithm many thousands of times on the problem instance.

By this metric, the Nearest Neighbor algorithm produced an excellent result for one of our TAP instances, but produced mediocre and poor results for the two others. The average quality of solutions from the Random Neighbor algorithm depends on how choices are randomized, which can be done in many ways. We have explored one way that uses a bias function that assigns probability weights to alternative choices depending on their cost.

We have not found a single bias function that outperforms all others on our TAP instances, but we found several that give a decent probability of finding a “top-tier” solution: that is, a solution of the highest cardinality with a cost not more than 10% higher than the winning solution from thousands of tests.

Although the top-tier probability can be low for a single use of Random Neighbor, one should get quite a good chance by repeating Random Neighbor thirty times.

For references and further exploration, download the full whitepaper. 

Download the full Whitepaper